Building a CPU in Verilog
1 Introduction
Field Programmable Gate Arrays (FPGAs) are complex re-configurable devices which can be programmed to implement certain application or functionality requirements via the use of digital circuits - their nature makes them very appealing for various markets, as they can be adapted to support different roles by simply being reprogrammed (Xilinx, n.d. (a)).
In the context of embedded systems, Nakano and Ito (2008) state that it is important to write efficient programs which are responsible for controlling the system, yet students often only understand high-level languages from the context of programs, where they may lack the knowledge of how a formula is evaluated or how advanced programming features such as pointers and stacks work on a hardware level. Despite their focus on embedded systems, the benefits of understanding advanced features and being able to write smaller, more efficient programs will always be desirable no matter how powerful computers get in the future.
This project aims to explore what knowledge is required to create a solution in Verilog, to apply that new knowledge to create a working processor and understand how these solutions provide a deeper understanding of the fundamental link between hardware and software. This exploration is beneficial as it utilises hardware which is in abundance in medical fields, automobiles, industrial control systems and many more (Tong et al, 2006) - this provides a perspective of what types of implementations are possible with such powerful and versatile hardware.
Furthermore, thanks to the abstractions provided by using a hardware description language (HDL), students would be able to draw from existing knowledge they may have of control flow, arithmetic operations and functions from languages such as Python, C# or C++ alongside using vendor-specific design suites to create and understand a design with relative ease.
2 Literature Review
2.1 Background
Nakano and Ito (2008) state that “for developing efficient programs, it is necessary to understand how programs are executed” elaborating later that “it is difficult to understand a […] ‘pointer’ if one does not know how it is implemented in a machine language” and suggest the idea of using FPGAs to teach students not only how pointers work, but to also introduce them to processor architecture, assembler & compiler design and assembler programming. Similarly, Lee et al (2012) also emphasise the importance of learning CPU design by stating that the “students acquire a deeper understanding of computer organization” and that it “profoundly increases their confidence with hardware” whilst also simultaneously providing a greater understanding of software optimisation. Furthermore, Yıdız et al (2018) make the point that without understanding the foundations of processors, it is not possible to understand advanced concepts such as “pipelining, memory hierarchy, branch prediction, caching etc.”, all extremely important concepts which have enabled the high computation power of modern-day processors.
These authors, and many more as cited by Yıdız et al (2018), have recognised the importance of teaching processor design and implementation, and the skills which students can gain from having such a deep understanding of a fundamental piece of modern computers. The goal of this project is to achieve exactly that – to understand processors at the lowest possible level by creating a complete, working CPU using Verilog, burning it onto an FPGA and going through the entire bug fixing and testing stage to ensure it works as expected.
The success of these proposed courses can be seen in the conclusions of the papers; Nakano and Ito (2008) had 18 students enrolled, with 15 partaking in a final exam to confirm their understanding of the material – they concluded that the students “have learned and understood CPU design […] very well.” (p. 728). Similarly, Lee et al (2012) performed a more comprehensive study into the effectiveness of their own proposed course, finding that the sentiment of 29 students regarding the statement “I understand CPU and computer systems much better than before” was a solid “agree”, illustrating the effectiveness of using FPGAs to learn CPU design (p. 347, table VII & table IX). University of Lincoln’s own Computer Architecture module may benefit from this work, by creating new practical workshops based upon it in the future.
Implementations of FPGA based CPUs (otherwise known as “soft processors” (Microsemi, n.d.)), vary between authors with some opting to use different word sizes such as 8, 16 or 32-bit, or even different instruction set paradigms such as CISC (complex instruction set computer), RISC (reduced instruction set computer) or with some opting for a custom ISA (instruction set architecture) as is the case of Nakano and Ito (2008) and their TINYCPU – but this is not an exhaustive list of possible features and implementation differences. That being said, possibly one of the most influential factors for an implementation would have to be deciding the instruction set for the processor – which dictates exactly what the processor is capable (or not capable) of doing, and the paradigm (such as CISC or RISC) which decides exactly how those instructions are executed by influencing the design of the hardware.
For example, a CISC based implementation will have instructions which take multiple clock cycles to complete, requiring microprograms/microcode in order to coordinate the execution of the instruction correctly. On the other hand, a RISC based implementation does away with complex multi-cycle instructions and the microcode hardware in favour for hardware logic, boiling down the instructions into simpler counterparts with a focus on ensuring approximately one instruction gets executed each cycle (Fox, n.d.; Elijhani and Kepuska, 2021).
2.2 Analysis of Existing Work
This section explores works which are relevant to the topic proposed by the project, and aims to derive a greater understanding of how an implementation may be created. It looks into the methodology, design decisions and reasoning made by those authors to understand the advantages and disadvantages of their approach. The goal is to have some form of reference or knowledge base in which informed design decisions can be made.
2.2.1 8-bit CISC
The implementation of the CPU and its supporting components such as the random access memory (RAM), as performed by Yhang and Bao (2011) are very similar to what one might see in a modern day x86-64 CPU – it shares its data/address bus between the arithmetic logic unit (ALU), registers and the RAM of the system, instead of using multiplexers and many wires to connect everything together. However, using a bus also increases complexity as the actions of the individual components must be coordinated in order to avoid race conditions.
More importantly, the factor which makes this architecture CISC based is its use of a microprogram controller – a piece of hardware which is used to coordinate instruction execution (as mentioned briefly above).
Their implementation uses a micro-instruction word width of 24-bits, consisting of two distinct field groups – an address field containing the address of the next micro-instruction, and an “operation controlling field” which is used to issue “micro commands” i.e., these fields will be setting the necessary control lines within the processor in order to achieve the desired instruction. Unfortunately, their table which demonstrates the format of the micro-instruction is slightly cryptic, however it is only the theory which is important. Furthermore, their flowchart which indicates each set of the microprogram is an ingenious way of visualising the appropriate steps required, and definitely something to use in this project (Yhang and Bao, 2011).
2.2.2 16-bit Architecture
The approach taken by Nakano and Ito (2008) with their TINYCPU is certainly very interesting: instead of taking a traditional approach of including an accumulator or a collection of registers for the developer to use, they opted for a stack instead - a stack being a data structure where information is “pushed” onto it and “popped” off where required, creating a last-in first-out situation (Koopman, 1989). The understanding of how a stack is implemented is out of the scope for this report, but it is an unconventional (but clearly working) way of implementing a processor, simply judging by the number of authors which opt for a register/accumulator-based processor instead.
As a result of this stack architecture, the operation codes (opcodes) for the TINYCPU lack any operands – this means that for load, store, arithmetic and logic operations, the element in the top of the stack (and sometimes the element immediately below it) is used. This is quite a novel idea compared to the others, however it unfortunately would be incompatible with the design plan set out in section 3.
One thing of significance to note is their implementation of the division operation, or rather, the lack of a specific opcode for it. As an example, Nakano and Ito (2008) implement an algorithm to prove the Collatz conjecture. The theory behind the conjecture is not important but the algorithm is. Provided with a number n, if it is odd then n = 3n + 1, else if n is even then n = n + 2. It can be seen that from the translated assembly code, that they use bit-shifting operations to divide or multiply by a power of 2, though it is unclear how this would function if you wished to multiply by any number which is not in that set – it is a possible compiler optimisation if required however (p. 726).
2.2.3 Video Graphics Array (VGA) Theory
VGA is an analog video hardware specification introduced by IBM which has reached far and wide, as it is still prevalent on nearly all computer monitors. Implementation of the VGA standard is trivial, which is excellent for creating some meaningful output. However it is important to remember that an FPGA is a purely digital device, and that the video signal for VGA is analog – there is a need for a physical digital to analog converter circuit (DAC) (Monk, 2017, p. 125).
A VGA signal is easy to understand – there are three wires for the colours (red, green and blue), one wire for the horizontal sync and another wire for the vertical sync. The RGB wires are analog and are expected to be driven in a range of 0V to 0.7V, whilst the horizontal and vertical sync wires are digital and can be driven between 0V to 3.3V (Monk, 2017, p. 125).
A core component of a VGA driver is the pixel clock – this provides a force that drives the entire system forwards, and when combined with counters to keep track of the x and y positions, it is able to determine what action the driver should be performing. For a resolution of 640x480, it is exactly driven at 25.175MHz (TinyVGA, 2008), however a higher clock would allow for a higher resolution.
2.2.4 Summary
The exploration of existing works by authors such as Nakano and Ito (2008) and Yhang and Bao (2011) help highlight the different possible approaches to creating a novel CPU architecture – their vastly different methods provide an insight into how the architecture may be structured and how this directly influences the available instruction set.
In particular, the implementation of a microprogram controller which Yhang and Bao (2011) present is of particular interest, as I believe that it is easier to understand the micro-steps/micro-instructions which the processor executes compared to understanding how to coordinate an entire instruction execution within one clock cycle – at least as a beginner with FPGAs and HDLs.
The brief introduction to the VGA standard is used to illustrate how simple the implementation of a video interface can be, given that external hardware is provided in order to draw the colours properly. The information gained from this research and the sources gathered are planned to be used to implement a rudimentary memory-mapped display driver – something akin to a graphics processor.
3 Design and Development
This chapter covers the design process of the CPU. Section 3.1 covers the basic theory behind CPU architecture and organisation, with an analysis of how it may affect the design and an examination of existing processors to determine their type. Section 3.2 applies the theory learned previously to design modules which make up the sub-components of the CPU, and are realised into the final design in section 3.3.
Section 3.2 applies the theory learned previously to design the modules which will end up becoming the sub-components of the CPU, with justification of why one approach was taken over another where applicable.
The design of the modules are realised in section 3.3 which hopes to provide a concise showcase of the final design, using Verilog and diagrams to showcase their function.
3.1 Design
A common goal between both the original project proposal and the final artefact was the creation of a working CPU – however it was important to decide on details of its function before any HDL could be written. It could be designed as a general-purpose CPU such as the MOS 6502 or the Manchester Baby, or it could be designed as a specialised processor which would be akin to a floating-point unit (FPU) on older hardware. It was decided that implementing a specialised processor would not be reasonable, as it is essentially a dedicated circuit for one function with the idea being that it performs that particular function very well and does it very quickly, but a general-purpose CPU should be able to perform the same function albeit at the cost of speed (PCMag, n.d. (a)).
Once the purpose of the CPU is decided, an abstract model can be created which defines precisely what the CPU is capable of – ARM (n.d. (a)) defines this as an “Instruction Set Architecture” (ISA) and states that the “ISA defines the supported data types, the registers, how hardware manages main memory, key features […], which instructions a microprocessor can execute, and the input/output model”. It is clear from this definition that creating an ISA is an important step to realising the goal of creating a CPU and therefore careful consideration must be given to the design.
3.1.1 Internal Organisation
Firstly, the internal storage of the CPU must be decided - this dictates how the CPU stores and manipulates data. There are multiple approaches to this: a stack architecture, an accumulator architecture, or a general-purpose register (GPR) architecture. To make an informed decision on which would be appropriate to use, the advantages and disadvantages must be recognised. Null and Lobur (2018, p. 582) summarise these different architectures as:
- Stack architectures use a stack (first-in-first-out (FIFO) memory model) to execute instructions and operands are found on the top of the stack. A simple model but the stack does not support random access, reducing the ability to create efficient code and will eventually become a bottleneck.
- Accumulator architectures store one operand in a specially designated register which allows for reduced complexity and short instructions, however the memory is temporary, and the register would experience increased traffic for every instruction executed.
- GPR architectures are the most common, using multiple registers (known as a register file or a register set) to execute a program. The additional registers allow for more efficient code and allow for faster execution time by reducing the number of times memory has to be accessed.
Null and Lobur (2018, p. 583) further explain that the GPR architecture type “can be broken down into three classifications, depending on where the operands are located” – this is another indicator of a processor being either CISC or RISC, as explained later. These three classifications are summarised below:
- Memory-memory: storing operands in memory and allowing an instruction to perform an operation without requiring any operand in the register.
- Register-memory: at least one operand is in a register and the other is in memory.
- Load-store: moving data from memory into registers before any operations can be performed.
Two of these three GPR architecture types in particular can be seen in modern processors – ARM (2005, p. A1-2) describes its architecture as being of the load-store type which is evident given that only the load and store instructions can modify memory. In contrast, Intel (and consequently AMD as they both implement the x86 ISA) are of the register-memory type as its ISA allows for the modification of memory directly but only if the other operand is present in a register (Null and Lobur, 2018, p. 627-628).
It was decided to use the GPR load-store type for this project as it would both provide a reasonable number of registers available to the programmer but also decrease complexity in terms of memory access – this allows for a more RISC-like behaviour from the CPU, whilst also having the benefit of making the instruction set clearer as opposed to the multiple possible permutations of memory access allowed by the x86 ISA; simple load and store instructions will handle memory access.
3.1.2 Key Features and I/O
To improve the chances of success, an attempt at keeping the design of the CPU as simple as possible should be made – complex functionality should not be implemented before the CPU itself is able to execute instructions without fault. As a result, very little time had been allocated to implementing I/O as there was an expectation that the core functionality would take some time to implement. Had there been more time, then a keyboard and video interface could have been implemented as the lack of it is a hinderance to the user.
A keyboard implementation can take many forms, perhaps utilising either the UART or PS/2 standard to transmit information; it also the most complex to implement as care has to be given to how a keyboard event is handled via an interrupt. A video interface would be much simpler to create, as it would only have to read from video memory to generate a picture, so this is the first interface to be implemented provided there is enough time remaining. The video interface chosen is VGA due to the limited clock provided by the FPGA developement board.
3.1.3 Instruction Set and Memory Model
There are multiple memory models which can be employed, however the two to focus on will be the flat memory model and the segmented memory model; Intel (2021, volume 1, p. 3-7) describes the flat memory model as memory appearing to a program “as a single, continuous address space” running from 0 to 2N-1 where N is the word size of the system. The segmented memory model however splits the physical memory into groups where they are then “mapped into the processor’s linear address space” and to access the data within a segment, “the processor […] translates each logical address [(consisting of a segment selector and offset)] into a linear address” and the reason for doing this would be to “increase the reliability of programs and systems” however as this project is creating an experimental CPU which will not be used outside of this project, it is not important to consider the long term reliability of the program and systems running it.
Therefore, the CPU is to use a flat memory model which can either be indexed by the control unit incrementing the Program Counter (PC), manipulated by the user using jump instructions or by using the previously mentioned GPRs as memory data registers (MDR) and memory address registers (MAR).
Verilog allows the parameterisation of module instances, such as creating registers of varying widths without the need to rewrite the code particular to that implementation – this allows for one single module to be coded, and then adapted to any situation i.e., creating a 16-bit register and an 8-bit register but using the same module code so that the behaviour of those registers is identical. The “word” size of a system is typically used to describe the natural unit for a given CPU (Fox, n.d.) – it specifies the width of data which the processor can handle at once, so the importance of the parameterisation is evident as it allows for experimental changes to the CPU word size.
The advantages and disadvantages of picking one word size over another are only apparent when there are functions of the CPU which would heavily benefit from having one particular size. Modern CPUs often have word sizes which are either 32 or 64-bits wide, however it seemed excessive for this project and thus some research was conducted into popular retro CPUs. The Intel 8080, MOS 6502, Zilog Z80, Motorola 6800 all used 8-bit words and were successful, with the aforementioned CPUs powering various types of 1980s computers such as the BBC Micro, Commodore PET and the Nintendo Entertainment System to name a few.
The CPU is to use an 8-bit word as its natural unit and therefore the registers, ALU and other components need to be created appropriately. However, it is not sufficient enough to encode data into 8-bits, as it lacks an instruction field meaning that the processor will not know what operation to perform. A solution to this is to encode the instruction into a bitfield larger than the word size of the CPU, which would provide additional bits that can be allocated to encoding the instruction – the size of this bitfield is dependent on how many instructions to be implemented or how the opcode is decoded, for example the Intel 8080 uses an 8-bit word internally but works with 16-bit instructions, whereas the MOS 6502 requires two cycles to fetch both the 8-bit instruction and operand if necessary (MOS, 1976, p. 60).
The final decision is for the CPU to use an 8-bit word size, with 16-bit wide instruction encoding – this would allow for mathematical operations using numbers between 0 to 255 (unsigned) or -128 to 127 (signed), and 256 unique instructions. Knowing the allowed size of the opcode now allows for the creation of the instruction encoding – it must consider multiple types of instructions, such as those which operate between registers, which use an immediate value, jumps and short instructions such as halt and no-operation (NOP) – the encoding of these instruction types are presented in figure 1.
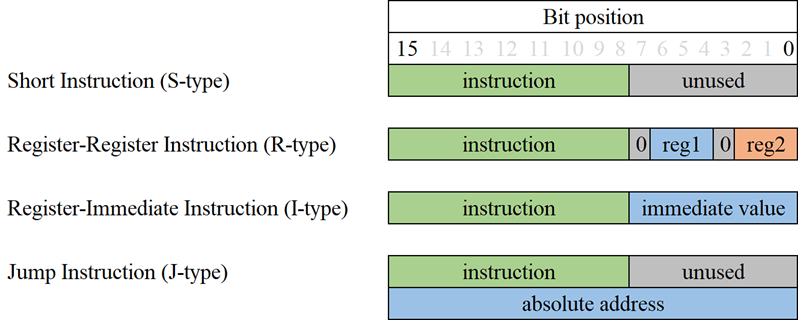
3.1.4 Summary
The CPU is to be designed with general-purpose registers, utilising a load-store architecture similar to that of ARM processors. It will operate on 8-bit words and use a 16-bit address space which will be linearly mapped to physical memory; each 16-bit word in memory will either encode data (such as a variable) or an instruction. There will be limited I/O with the processor, but if time permits, then there will be a focus on implementing video first. The instruction set of the CPU should reflect its general-purpose nature.
3.2 Design Decisions
This section explores the design decisions made for the core modules, and the rationale behind it.
3.2.1 Control Unit
A control unit coordinates the actions of the CPU, such as instruction fetching/decoding and the execution of an instruction (Fox, n.d.). Most importantly, there are two design paradigms, RISC vs CISC, which come into play - they affect the design of the control unit and its method of executing an instruction.
ARM, which implements RISC architectures, has a set of different instruction types which are densely packed with information in order to tell the processor how to appropriately execute it (ARM, 2005, p. A3-2) - this avoids the use of firmware such as microcode and allows ARM to use hardware to accelerate instruction execution. The information density and the variability of the instructions would bring too much complexity to the project, so a more traditional approach with microcode was taken.
Disadvantages of microcode is that it both increases execution time for an instruction, as it requires multiple clock cycles to step through the total number of micro-instructions for one instruction (as shown by the codeblock below), and also that it requires the developer to write the firmware, requiring additional testing to ensure that it is executing as expected and that it is also not interfering with other instructions.
krisjdev/tau-processor/mem_init/microcode.mem
Lines 27 to 30 from dissertation-copy
| 27 | 0800 // nop @ 0 - 0 |
| 28 | 8800 // hlt @ 1 - 1 |
| 29 | 0016 0808 // mov reg1, reg2 @ 2 - 3 |
| 30 | 0026 0800 // cmp reg1, reg2 @ 4 - 5 |
In order to coordinate the actions of all components, not only within the control unit but also other sub-components of the CPU, a finite state machine (FSM) is used - this is represented as the “Execution Driver” in figure 4. Wilson and Mantooth (2013, p. 174) state that the “idea of an FSM is to store a sequence of different unique states and transition between them depending on the values of the inputs and the current state of the machine” and that an FSM can be one of two types: “Moore (where the output of the state machine is purely dependent on the state variables) and Mealy (where the output can depend on the current state variable values and the input values)”.
3.2.2 Arithmetic Logic Unit (ALU)
The ALU is the heart of all mathematical operations, both arithmetical and logical - a design may implement integer addition, subtraction, multiplication and division with logical operations such as AND, OR, NOT or XOR. Furthermore, the ALU modifies a status (or “flag”) register, which stores information about the outcome of the operation such as whether the operation had overflowed, resulted in a zero, has a carry or is a negative value (Fox, n.d.).
Thanks to the high-level abstractions provided by Verilog, the code for the ALU was both easy to write and its C-like syntax is easy to understand. The use of constructions such as functions allow the developer to re-use code wherever it is deemed necessary, without worry of how the final circuit would turn out as this is handled with Quartus Prime. However, this abstraction comes at a significant cost - there is simply no transparency with what has been synthesised onto the silicon, meaning the users have to trust that it is safe, secure and will function as described.
To ensure that the flags were set appropriately for whichever operation was executed, the Intel Software Architectures Manual (2021, p. A-1) was referenced – this ensured that the behaviour was consistent across two different types of architectures, which would make the operation of the ALU predictable.
As the ALU does not differentiate between signed and unsigned arithmetic, its functions are easy to implement and it is down to the software programmer to interpret the result of the calculation – this is the sign flag as illustrated in both figures 5 and 6. This is possible due to two’s complement which is a method which uses one bit in the word to indicate whether the value is positive or negative – it is calculated by taking a value as bits, inverting it, and adding one (Fox, n.d.).
3.2.3 Memory, Memory Controller and Datapath Controller
Memory can be seen in all computing systems – it stores the program to be executed and any data required for it, however there are multiple methods of organising this system. Eigenmann and Lilja (1998) explain that a “Von Neumann” type organisation is where “instructions and data are stored together in common memory” which distinguishes it from the “Harvard” type “in which separate memories are used to store instructions are data. Typically, Harvard-type architectures can be found in microcontrollers in embedded systems such as appliances or toys and many non-Von Neumann-type architectures can be found in specialist applications ranging from image and digital signal processing to implementing neural networks, cellular automata or cognitive computers or silicon (Null and Lobur, 2018, p. 136 - 137).
As the aim of this project is to build a general-purpose processor, utilising an architecture such as Harvard is non-sensical, as the instructions and data are stored separately which would result in increased complexity; for this reason, the processor uses a Von Neumann architecture. Null and Lobur (2018, p. 131) describe it as a system which has the following characteristics:
- Has a control unit, ALU, registers, program counter, a memory system which contains the programs and an I/O system.
- Has the capacity to carry out sequential instruction processing.
- Contains a single path, either physically or logically, between the main memory system and the control unit of the processor.
Aside from deciding the memory architecture of the system, some thought must be given to how the CPU can translate an instruction into a memory access. For this, a memory controller is proposed – this will sit before the memory and act as an interface which will handle the loading and storing of values in the right memory block.
Furthermore, the implementation of the jump instruction is unique compared to others (discussed more in section 3.2.4) and therefore requires additional logic in order to execute correctly. To get the right address, the system must first peek ahead in memory by one address and fetch this value however, with a single output line from the system memory, it could end up overwriting the current instruction. For this, the datapath controller will handle splitting the instructions from addresses and miscellaneous data which is being loaded.
3.2.4 Decision Unit
The “Decision Unit” is a circuit which determines the correct address to jump to when a jump instruction is executed, based on the state of the instruction and the ALU flags register.
An oddity of the system is that it implements an absolute addressing mode, so the entire address must be specified unlike in relative addressing mode, where the current instruction address is considered (IBM, 2022). To ensure that the programmer the programmer has access to the entire 216 -word address space, additional circuitry (as described in section 3.2.3) was implemented to allow the system to read 32-bits specifically for jump instructions - 16 bits are used to describe the opcode as usual, and the other 16-bits are the address to jump to if the conditions are met.
Furthermore, if the conditional jump fails, it is important to ensure that the CPU does not accidentally execute the value of the address so even on a failed conditional jump, the program counter is incremented by two, skipping both the instruction and its address value.
For conditional jumps, the decision unit checks the flag states in a similar method to the x86 implementation, as shown in table 2 from the Intel Software Architectures Manual (2021, p. 7-16). This allows for the behaviour of the jump instructions and the decision unit to be predictable and consistent across two different types of architectures, similar to the ALU.
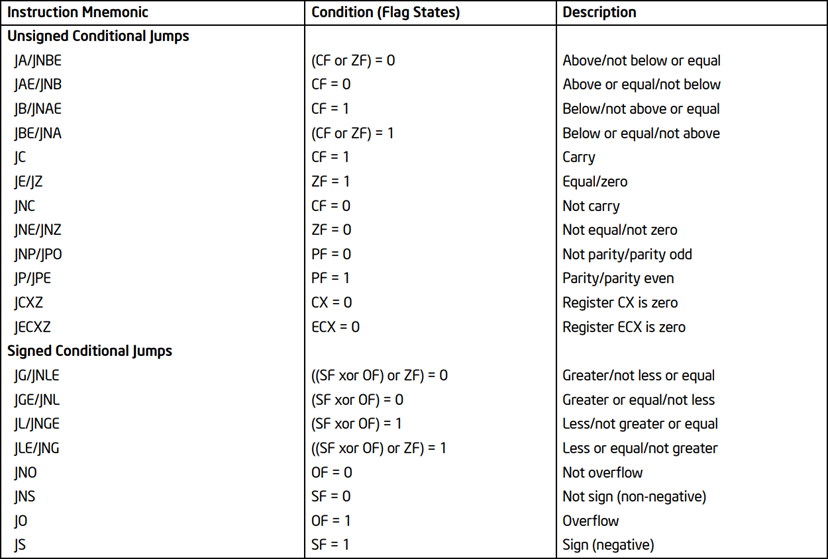
The processor implements all jumps except for JNP/JNO, JP/JPE, JCXZ or JECXZ as it does not contain the hardware specific to those jumps.
3.2.5 Video Graphics Array (VGA)
Memory available on the FPGA is limited, but in order to draw colours onto the screen, either an additional memory module had to be installed (requiring an interface with external hardware) or to reduce the resolution and use the remaining space for colour information. As such, it was decided to drive the VGA signal at a resolution of 320x240, exactly half of the industry standard of 640x480, which is not a recognised signal so whilst the driver runs the monitor at 640x480, additional logic is required to upscale the resolution so that it is displayed properly. The colours themselves are allocated 4 bits, totalling to 16 unique colours with the help of additional circuitry.
The upscaling logic uses the x and y position counters to determine which address of the video memory to index, and presents the output in the form of pixel information which is fed into a colour look-up table and finally output to the monitor. The upscaling logic also acts as a buffer as the memory can only return a 16-bit value, and at a colour depth of 4-bits (meaning 4-bits per pixel), each new line from the video memory is encoding 4 pixels at once. The logic must be capable of upscaling the output and coordinating video memory access based on the incoming x and y counters.
3.3 Final Design
3.3.1 Control Unit
Microcode was the choice for this project, as it is easier to grasp the concept that multiple micro-instructions make up one entire instruction - these micro-instructions set the control lines for the CPU sub-components, and can be easily converted into regular bytes which are written to the microcode read-only memory (ROM).
A microcode format is presented in figure 3, showcasing the bitfield available to micro-instruction to manipulate in order to achieve its specified goal. It consists of multiple fields which either set flags for functions such as jumping or finishing an instruction, to controlling which mode a module is set to. The micro-instruction may manipulate the memory controller, datapath controller and the ALU (all discussed in later sections) to perform actions such as loading, adding and jumping.
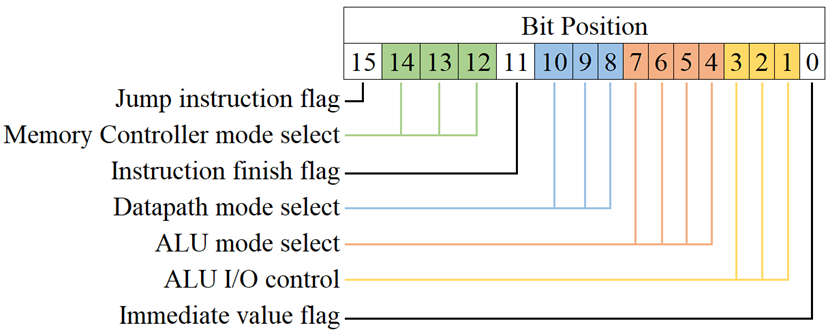
The microcode ROM is only one module in an entire system which makes up the control unit for this CPU, and therefore we must look at the rest of the system, as shown in figure 4.
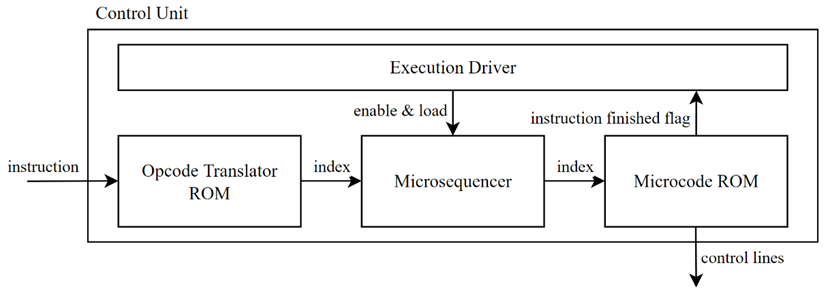
The “Opcode Translator ROM” receives an instruction, where it then decodes the opcode and uses it as an index for its own memory - this will return an appropriate value for the microsequencer in order to begin executing the instruction. As instructions can take multiple cycles to execute, the microsequencer acts as a counter where it will begin counting from the provided index until the instruction finished flag is raised. This also enables truly variable execution length instructions without the risk of the microsequencer indexing illegal microinstructions in the microcode ROM.
The execution driver module is a Mealy-type FSM - it tracks the current state of the machine using a register, but also have multiple input signals which can allow the machine to switch states as illustrated by the “instruction finish flag” line in the figure 4. The possible states (and a description of them) of the execution driver are illustrated in table 1.
| State Value | State Name | Description |
|---|---|---|
| 0 | Cold Boot | Initial state - buffering for a clock cycle to ensure the instruction is ready. |
| 1 | Loading Instruction | Loading the microsequencer with the correct value and enabling the microcode ROM. |
| 2 | Long/Short Instruction Execution | Checking whether the instruction finish flag is raised - if true then the machine executed a short instruction (one microinstruction) else the machine is executing a long instruction (two or more microinstructions). |
| 3 | Reset or Continue | If the instruction was short, all the control lines for the program counter, microsequencer and microcode are set appropriately. Otherwise, if the instruction is long, then the machine remains at the state until the finished flag is raised. |
| 4 | Finish Execution | Prepares the machine for the next instruction. |
| 5 | Halt | Halt state prevents execution from occurring - this can only be exited by resetting the processor. |
| 6 | Jump | Handles the control lines for loading the microsequencer and program counter with the new index and address, respectively. |
3.3.2 Arithmetic Logic Unit (ALU)
The ALU is implemented via the use of multiple high-level Verilog constructions, namely the ability to define functions and switch-case statements. The use of functions is best suited for actions which are repetitive, such as for when multiple operations modify the flags register, as illustrated by a function definition in figure 5, and a function call in an ALU operation in figure 6.
krisjdev/tau-processor/src/alu.sv
Lines 28 to 31 from dissertation-copy
| 28 | function is_signed (input [WORD_SIZE-1:0] A); begin |
| 29 | is_signed = A[7]; |
| 30 | end |
| 31 | endfunction |
krisjdev/tau-processor/src/alu.sv
Lines 144 to 152 from dissertation-copy
| 144 | // add = a + b |
| 145 | 6: begin |
| 146 | //temp = a + b; |
| 147 | output_C = input_A + input_B; |
| 148 | flags[ZERO] = is_zero(output_C); |
| 149 | flags[SIGN] = is_signed(output_C); |
| 150 | flags[CARRY] = has_carry_add(input_A, input_B); |
| 151 | flags[OVERFLOW] = has_overflow(input_A, input_B); |
| 152 | end |
As shown by figure 6, flags are modified by calling a function to determine the state of the flag, and then this value is used to update the appropriate bit in the flags register. It is important that these values are updated correctly depending on which ALU operation was executed, as these values are referenced when executing conditional jump instructions.
Furthermore, the switch-case construct provides an easy method of implementing multiple operation codes which can be used on any number of incoming signals. In the case of this project CPU, the ALU is controlled by the microcode and selects the appropriate operation based on the instruction. An example of this is given in figure 7.
krisjdev/tau-processor/src/alu.sv
Lines 93 to 110 from dissertation-copy
| 93 | always_comb begin |
| 94 | case(mode_select) |
| 95 | |
| 96 | // do nothing |
| 97 | 0: output_C = output_C; |
| 98 | |
| 99 | // move B into C |
| 100 | 1: output_C = input_B; |
| 101 | |
| 102 | // compare a & b |
| 103 | 2: begin |
| 104 | temp = input_A - input_B; |
| 105 | $display("ALU CMP TEMP A - B = C --- %h - %h = %h", input_A, input_B, temp); |
| 106 | flags[ZERO] = is_zero(temp); |
| 107 | flags[SIGN] = is_signed(temp); |
| 108 | flags[CARRY] = has_carry_subtract(input_A, input_B); |
| 109 | flags[OVERFLOW] = has_overflow_subtract(input_A, input_B); |
| 110 | end |
3.3.3 Memory, Memory Controller and Datapath Controller
The main system memory is implemented as a single port RAM as illustrated in figure 8; its size can be reconfigured based on how it is instantiated via Verilog, however as the processor is designed to work with 16-bit instructions, the RAM has a 16-bit word width with 216 total possible locations which can be accessed - this translates into 65,536 words or a total of 128KiB of memory.
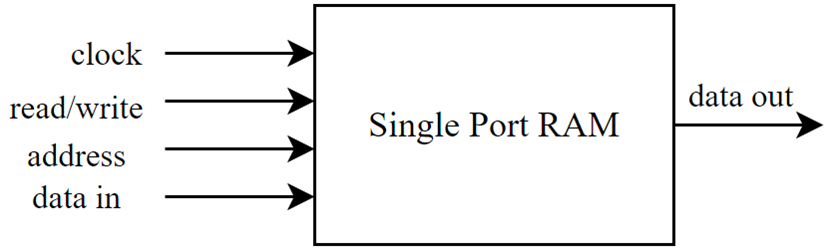
A requirement for the processor is for it to generate a valid VGA signal and to successfully draw an image on the screen - this is discussed more in section 3.3.6 however it is being brought up now because the image is actually memory mapped, meaning video memory (VRAM) must be allocated on the FPGA as well. The requirements are that the resolution is 320x240 with 4-bit colour depth - this results in 320x240x4 = 307200 bits required for the image which is 37.5KiB or 19,200 words.
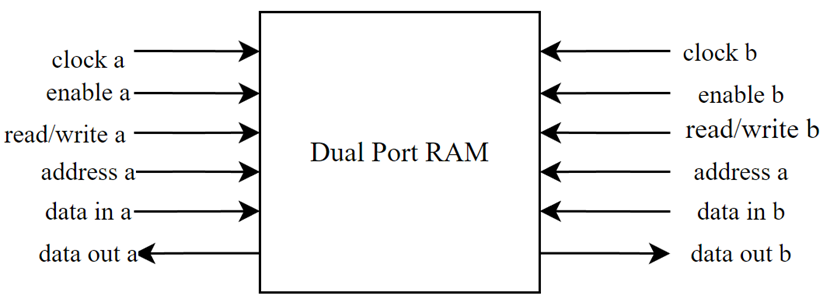
Furthermore, the VRAM is unique in its construction when compared to the system RAM, as it is a dual port RAM module as opposed to a single port RAM - that is, it can be driven by two clocks, have two different addresses reading and writing data (nandland, n.d.). A dual port RAM module was created for use as VRAM as it would allow for mismatched clocks to operate on the RAM block, meaning that the function of the display output is not hindered if the CPU is run at anything other than the required frequency of the VGA signal.
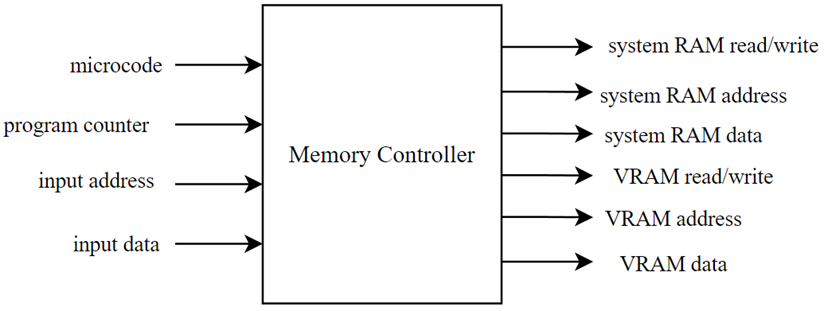
Memory is no good if the processor has no method to access the data stored on it, so a dedicated memory controller module was created in order to coordinate access between both the system RAM and VRAM. Additional functionality was implemented in the module in order to assist with functions such as jumping to different addresses (explained in section 3.2.4), storing values in memory and loading values from memory by setting the correct control lines.
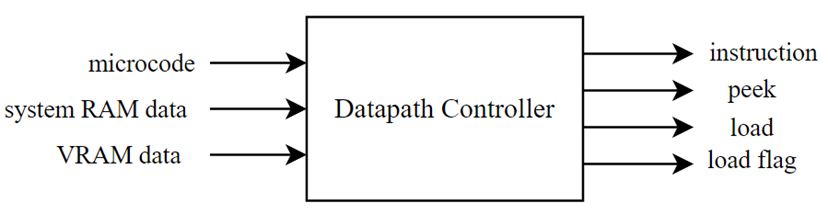
Further additional logic was implemented in the form of a datapath controller - this module connects to the outputs of both the system RAM and VRAM and helps correctly coordinate information around to the appropriate busses. The datapath controller acts similarly to a multiplexer, where it dictates the flow of data depending on an input, however it is vital that information is correctly routed - a loaded value should not cause the current instruction line to change, as it could cause unexpected behaviour. In conjunction with the aforementioned memory controller module, they work together to enable the jump, load and store class of instructions.
3.3.4 Decision Unit
Similar to the ALU, the implementation of the decision unit is built using a switch-case statement which is triggered when the right opcodes are executed. It requires thhe current address from the program counter, the destination address fetched from memory and the ALU flags to be input before it can decide on the correct address to jump to. As mentioned in section 3.2.4, if a conditional jump instruction fails, the program counter still needs to be incremented by two in order to not accidentally execute the address for a jump instruction. This is due to the jump instruction being 32-bits long instead of the regular 16-bits, so therefore the result for a failed conditional jump is always program_counter = program_counter + 2, as shown in figure 12.

Figure 13 shows how the logic for a conditional and unconditional jump is implemented in the decision unit.
krisjdev/tau-processor/src/decision_unit.sv
Lines 31 to 37 from dissertation-copy
| 31 | always @ (instruction or peek_jump_address or flags) begin |
| 32 | case (instruction[15:8]) |
| 33 | |
| 34 | JMP: new_address = peek_jump_address; |
| 35 | |
| 36 | JE: new_address = (flags[ZERO] == 1) ? peek_jump_address : program_counter_address+2; |
| 37 | JNE: new_address = (flags[ZERO] == 0) ? peek_jump_address : program_counter_address+2; |
Two simple programs are presented in figures 14 and 15 with their accompanying simulation waveforms from ModelSim in figures 16 and 17 respectively; these figures help to illustrate the behaviour described previously. The program itself is simply moving a value into a register (line 1) and then comparing the value in the register with an immediate value (line 2); depending on the result of the comparison (which has modified the ALU flags) will decide which address the processor jumps to.
Full file (local copy)
| 1 | 2805 // mov a, 5 |
| 2 | 3005 // cmp a, 5 |
| 3 | 1500 // je 0008 |
| 4 | 0008 // (address) |
| 5 | 0000 // nop |
| 6 | 0000 // nop |
| 7 | 0000 // nop |
| 8 | 0000 // nop |
| 9 | 0100 // halt (jump target) |
Full file (local copy)
| 1 | 2805 // mov a, 5 |
| 2 | 3006 // cmp a, 6 |
| 3 | 1500 // je 0008 |
| 4 | 0008 // (address) |
| 5 | 0100 // halt |
| 6 | 0000 // nop |
| 7 | 0000 // nop |
| 8 | 0000 // nop |
| 9 | 0100 // halt (jump target) |


It can be seen from the simulation waveform figures 16 and 17 that the CPU has successfully jumped to the appropriate address given the result of the previous instructions.
3.3.5 Glue Logic
PCMag (n.d. b)) defines “glue logic” as “a simple logic circuit that is used to connect complex logic circuits together” - instances of these circuits can be seen all throughout the project in different forms. For example, some circuits act as decision logic for the multiplexers which help select the correct input based on the instruction as seen in figure 19, another circuits acts as a lookup-table to provide 16 different colours for the video output as seen in figure 20, and another circuits handles the logic required for the halt instruction, as shown by figure 18.
krisjdev/tau-processor/src/misc.sv
Lines 1 to 40 (edited) from dissertation-copy
| 1 | module halt_check # ( |
| 2 | parameter OPCODE_SIZE = 8 |
| 3 | ) ( |
| 4 | input wire [OPCODE_SIZE-1:0] opcode, |
| 5 | output reg result |
| 6 | ); |
| 7 | always_comb begin |
| 8 | if (opcode == 8'h01) begin |
| 9 | result = 0; |
| 10 | end else begin |
| 11 | result = 1; |
| 12 | end |
| 13 | end |
| 14 | endmodule |
krisjdev/tau-processor/src/reg_immN_control.sv
Lines 75 to 109 from dissertation-copy
| 75 | module muxer_select_decision_logic_b # ( |
| 76 | parameter WORD_SIZE = 16, |
| 77 | parameter DEFAULT_IMM_SELECTOR_VALUE = 0 |
| 78 | ) ( |
| 79 | input wire [WORD_SIZE-1:0] instruction, |
| 80 | input wire imm_flag, clock, |
| 81 | output reg [3:0] mode_select |
| 82 | ); |
| 83 | |
| 84 | // always_comb begin |
| 85 | // always @ (negedge clock) begin |
| 86 | always @ (instruction) begin |
| 87 | |
| 88 | // if the instruction contains an immediate value |
| 89 | if (instruction[15:8] >= 8'h28 & instruction[15:8] <= 8'h8f) begin |
| 90 | mode_select <= DEFAULT_IMM_SELECTOR_VALUE; |
| 91 | // if the instruction does not contain an immediate value but affects the registers |
| 92 | end else if (instruction[15:8] >= 8'h06 & instruction[15:8] <= 8'h13) begin |
| 93 | mode_select <= {1'b0, instruction[2:0]}; |
| 94 | end else begin |
| 95 | mode_select <= 'z; //mode_select; |
| 96 | end |
| 97 | |
| 98 | |
| 99 | //if (instruction[15:8] >= 8'h28 & instruction[15:8] <= 8'h8f) begin |
| 100 | // if (imm_flag == 1) begin |
| 101 | // mode_select <= DEFAULT_IMM_SELECTOR_VALUE; |
| 102 | // end else if (imm_flag == 0) begin |
| 103 | // mode_select <= {1'b0, instruction[2:0]}; |
| 104 | // end |
| 105 | //end else begin |
| 106 | // mode_select <= mode_select; |
| 107 | //end |
| 108 | end |
| 109 | endmodule |
krisjdev/tau-processor/src/misc.sv
Lines 68 to 104 from dissertation-copy
| 68 | module ega_colour_palette_logic ( |
| 69 | input wire [3:0] index, |
| 70 | output reg [5:0] colour |
| 71 | ); |
| 72 | |
| 73 | always_comb begin |
| 74 | |
| 75 | case (index) |
| 76 | // https://en.wikipedia.org/wiki/Enhanced_Graphics_Adapter#Color_palette |
| 77 | |
| 78 | // formatting is rgbRGB where lowercase = low intensity, uppercase = high intensity |
| 79 | // 5 4 3 2 1 0 |
| 80 | // r g b R G B |
| 81 | 0: colour <= 6'b000000; // black |
| 82 | 1: colour <= 6'b000001; // blue |
| 83 | 2: colour <= 6'b000010; // green |
| 84 | 3: colour <= 6'b000011; // cyan |
| 85 | 4: colour <= 6'b000100; // red |
| 86 | 5: colour <= 6'b000101; // magenta |
| 87 | 6: colour <= 6'b010100; // brown |
| 88 | 7: colour <= 6'b000111; // white/light grey |
| 89 | 8: colour <= 6'b111000; // dark grey / bright black |
| 90 | 9: colour <= 6'b111001; // bright blue |
| 91 | 10: colour <= 6'b111010; // bright green |
| 92 | 11: colour <= 6'b111011; // bright cyan |
| 93 | 12: colour <= 6'b111100; // bright red |
| 94 | 13: colour <= 6'b111101; // bright magenta |
| 95 | 14: colour <= 6'b111110; // bright yellow |
| 96 | 15: colour <= 6'b111111; // bright white |
| 97 | default: colour <= 0; |
| 98 | |
| 99 | endcase |
| 100 | |
| 101 | end |
| 102 | |
| 103 | |
| 104 | endmodule |
3.3.6 Video Graphics Array (VGA)
This clock required for VGA is achieved by using a phase locked loop (PLL) within the FPGA, which is provided as an intellectual property (IP) package by Altera. Counters which track the x and y position on the screen are set accordingly on each rising edge of the pixel clock. It is important to note that despite running the screen at 640x480, the counters are required by the specification to count above those values – this is due to the need for blanking intervals as the signal was originally developed with CRT monitors in mind, which would require time to reposition the electron gun so that the image was drawn correctly; these blanking intervals are illustrated in figure 21.
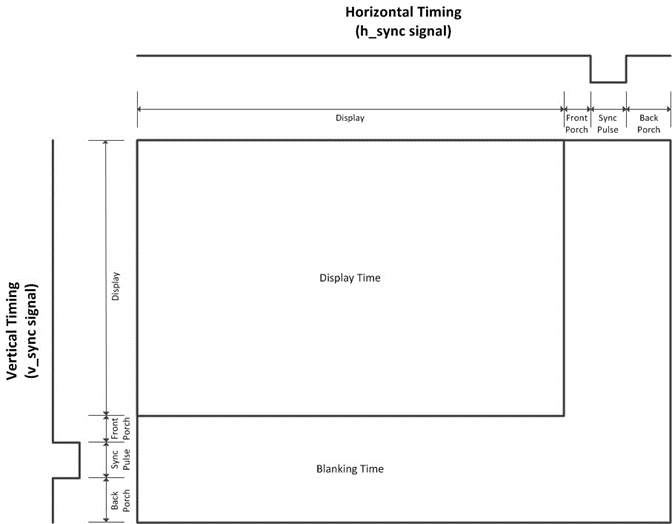
TinyVGA (2008) provides the timing information required to correctly drive the VGA display, such as the counts for the front & back porch and precisely how long the sync pulse must be. A Verilog implementation for a VGA driver can be seen in figure 22.
krisjdev/tau-processor/vga_driver.sv
Full file from dissertation-copy
| 1 | module vga_driver ( |
| 2 | input wire clock_25mhz, |
| 3 | output reg [9:0] x, y, |
| 4 | output reg hsync, vsync, in_active_area |
| 5 | ); |
| 6 | |
| 7 | initial begin |
| 8 | x <= 0; y <= 0; |
| 9 | end |
| 10 | |
| 11 | assign in_active_area = (x <= 639 && y <= 479); |
| 12 | assign hsync = ~(x >= 655 & x <= 751); |
| 13 | assign vsync = ~(y >= 489 & y <= 491); |
| 14 | |
| 15 | always @ (posedge clock_25mhz) begin |
| 16 | |
| 17 | if (x == 799) begin |
| 18 | x <= 0; |
| 19 | y <= (y == 524) ? 0 : y + 1; |
| 20 | end else begin |
| 21 | x++; |
| 22 | end |
| 23 | |
| 24 | end |
| 25 | |
| 26 | endmodule |
From figure 22 it can be seen that the module uses both continuous assignment with the “assign” keyword but also sequential logic due to the use of a clock. On every positive edge of the clock, the module will generate an output determined by the state of both the x and y registers. If x=799 then it indicates the end of a line, so the x counter is reset, and depending on the value of y depends which value it gets set to, as if y=524 then it would indicate the end the screen and it would get reset.
The continuously driven values ensure that the signals are always valid, which is vital for the h-sync and v-sync signals as this is how it synchronises with the monitor itself.
4 Evaluation
4.1 Testing
The importance of testing cannot be understated for any FPGA project – the time taken for the design suite to compile, synthesise and fit the design is considerable compared to simply running a simulation; therefore, testing was performed in two ways – via Verilog “testbenches” with ModelSim, and physically burning the design onto the FPGA and connecting to its pins.
Firstly, Verilog testbenches are created for every module present in the system; these testbenches are similar to the modules themselves, but the code instead instantiates the module which is under testing, and probes its input and output ports. In conjunction with simulation software, it is possible to analyse the input and output waveforms to determine whether the module is functioning as expected.
The difficulty of this testing scales as the project gets more complex, as testbenches need to be made which represent the final system in order to analyse how each module interacts with others – this results in a significant increase in the signals which need to be analysed to debug behaviour, both increasing complexity and time required. Furthermore, this type of analysis will simply be unable to cover all possible input permutations, which may result in some edge case bug not being discovered – it is possible to write specific test cases for these edge cases but it requires the developer to be aware of them.
The second method of testing utilised in this project was only used for determining whether the VGA signal and colour was being generated properly – this was quickly determined depending on whether or not the monitor would successfully recognise the signal. If successful, the test would show that the VGA driver and VRAM worked as expected, else the traditional functional analysis as described above would be used to determine the exact fault of the system.
An alternative to these methodologies would be “formal verification, where it is rigorously proved that the system functions correctly on all possible inputs” (Harrison, n.d.). Harrison (n.d., p. 2) continues, stating that “this involves forming mathematical models of the system and its intended behaviour, and linking the two”. This form of testing is more much likely to find issues with the design compared to the functional analysis, however the skills and knowledge to be able to determine which type of formal verification to use, how to appropriately apply it to the project and to interpret its results is far out of the scope of this project; this means that despite all the testing attempts, there is a chance that there may be a bug in the design which simply has not been discovered due to the right conditions not being met for it.
4.2 Operation
It is impossible to concretely state whether the CPU will function as expected for every possible input permutation, as discussed in section 3.3.1, however despite this, we can write code and then analyse the output and determine from that whether the CPU operates in a predictable manner.
A simple program is illustrated in figure 24 - it loads register A with 0 and register B with 1, performs an addition A = A + B and then halts.
Full file (local copy)
| 1 | 2800 // mov a, 0 |
| 2 | 2901 // mov b, 1 |
| 3 | 0b01 // add a, b |
| 4 | 0100 // halt |
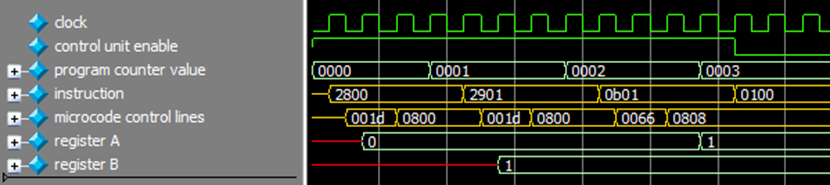
It can be seen from the waveforms presented in figure 25 that the outcome of the program is exactly what we have expected – the register A is initialised to the value 0, and then the CPU performs 0 + 1 = 1, and stores the result in register A.
A variant of the program previously is presented in figure 26 – this program initialises register A with the value 0, and then repeatedly adds 1 to register A via the use of jumps.
Full file (local copy)
| 1 | 2800 // mov a, 0 |
| 2 | 2901 // mov b, 1 |
| 3 | 0b01 // add a, b |
| 4 | 1400 // jmp |
| 5 | 0002 // (address) |
| 6 | 0100 // halt |

The final waveform for the program presented in figure 27 showcases that the CPU is capable of handling unconditional jumps – due to the way the CPU is designed, this functionality also extends to conditional jumps.
A more complex program is presented in figure 28 – this implements the Fibonacci sequence as described by Chandra and Weisstein (2022): Fn = Fn-1 + Fn-2 where Fn = F2 = 1, and by convention F0 = 0. The expected output for this equation is 1, 1, 2, 3, 5, 8, 13, 21 … and so on, as it continues to grow to infinity. This sequence is implemented in figure 28, and the output of the program is again presented as a waveform in figure 29.
Full file (local copy)
| 1 | 2800 // mov a, 0 |
| 2 | 2901 // mov b, 1 |
| 3 | 0621 // mov c, b |
| 4 | 0b10 // add b, a |
| 5 | 0602 // mov a, c |
| 6 | 0621 // mov c, b |
| 7 | 0b10 // add b, a |
| 8 | 30e9 // cmp a, 233 |
| 9 | 1500 // je |
| 10 | 000c // (address) |
| 11 | 1600 // jmp |
| 12 | 0004 // (address) |
| 13 | 0620 // mov c, a |
| 14 | 0100 // halt |

It can be seen by the contents of register C that the CPU has successfully executed the Fibonacci sequence program and has gone to the highest value that can fit into the 8-bit register – a comparison instruction and a conditional jump are used to detect this state and will jump to the halt instruction to prevent overflowing. This complex program implements the use of multiple registers, arithmetic operations with both immediate and register-stored values, comparison instruction and both conditional and unconditional jumps.
Furthermore, the CPU implements instructions (see appendix A) which enable it to load and store values from both system and video memory – a use of the load instruction on system memory is showcased below, however the principle is the same for the other types of memory access instructions.
Full file (local copy)
| 1 | 2c00 // mov e, 0 |
| 2 | 2d04 // mov f, 4 |
| 3 | 2801 // mov a, 1 |
| 4 | 0200 // load |
| 5 | 0b50 // add f, a |
| 6 | 0300 // store |
| 7 | 0100 // halt |
| 8 | beef // data |
| 9 | 0000 // target memory location |

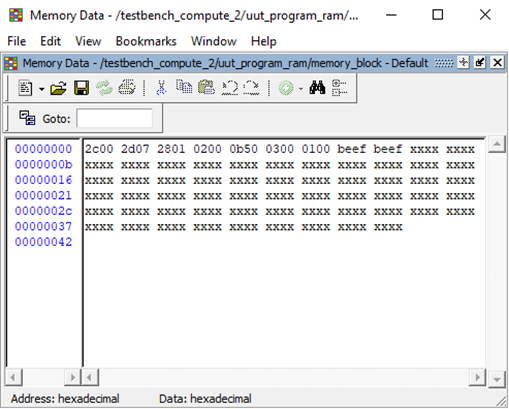
The steps taken to execute the program can be seen by the “control line” signal, present in every waveform above; these signals correspond to the microcode format presented in figure 3, and can be decoded in order to determine exactly what micro-instruction the CPU was performing to achieve the operation requested.
As mentioned in section 3.2.1, microcode increases execution time as it requires multiple clock cycles to step through each micro-instruction – as a result, it is difficult to determine the performance of the CPU as it depends entirely on the program composition. For example, a NOP instruction has one micro-instruction, an ADD instruction has two, LOAD has five and any jump instruction has three. Therefore, a program composed of purely NOPs would execute considerably faster than a program composed of LOADs – despite this, it is unrealistic to expect these types of programs they are non-functional in the sense that they do not compute anything. A more realistic expectation of performance would fall anywhere between the time it takes to execute a NOP and the time it takes to execute a LOAD instruction.
This performance can be quantified by calculating the number of instructions which the processor executes per second, IBM (1995, 6-9) provides an equation for MIPS (short for “Million instructions per second”) as follows: MIPS = clock / clocks per instruction x 10^6
An assumption will be made that the clock rate will be fixed to 50MHz (50,000,000Hz) as this is the maximum clock speed available on the FPGA development board. The number of cycles an instruction takes to execute is determined from the simulation waveforms.
A NOP instruction takes 3 clock cycles to execute, therefore a program consisting of all NOPs (or equivalent length instructions) has a MIPS of: MIPS(NOP) = 50,000,000 / 3x10^6 = 16.67
An ADD instruction takes 4 clock cycles to execute, therefore a program consisting of only ADDs (or equivalent length instructions) has a MIPS of: MIPS(ADD) = 50,000,000 / 4x10^6 = 12.50
A LOAD instruction takes 7 clock cycles to execute, therefore a program consisting of only LOADs (or equivalent length instructions) has a MIPS of: MIPS(LOAD) = 50,000,000 / 7x10^6 = 7.14
This fails to account for the fact that both E and F registers must be loaded with the appropriate address before a LOAD instruction can occur, and therefore the true MIPS would be lower as it takes 15 cycles to execute both move instructions and to load: MIPS(MOVE&LOAD) = 50,000,000 / 15x10^6 = 3.33
The MIPS metric itself can be misleading, as it does not account for some key factors when it comes to performance as described by IBM (1995):
- MIPS cannot be used to compare machines with different ISAs.
- MIPs cannot compare different programs on the same computer, as the instructions used to execute the program could vary drastically.
As a result, it is difficult to accurately compare the performance of this CPU to others in its class – perhaps a combination of multiple metrics would prove to be a better judge of performance.
5 Conclusion
To conclude, the project successfully achieves the aims set out in the introduction and presents a functional CPU which is capable of executing user programs without fault, as presented in sections 3.3.4 and 4.2. As a result of this success, invaluable knowledge about CPU organisation was gained which leads to a greater understanding of the fundamental link between hardware and software.
This flexibility provided by FPGAs lends itself to an incredibly steep learning curve – not only does the developer have to both learn the tools at hand and also understand how those tools assist in reaching the goal, but they must also be able to explore the problem space for their particular task and derive a series of steps which can successfully lead them to the end goal. In the context of this project, an understanding of the inner workings of a CPU was gained by researching multiple CPU architectures and examining their behaviour, available architecture documents and other pieces of information available around the internet – the culmination of this information was then used to influence the final design of the CPU.
The architecture of a processor is often hidden away from the end user, through mountains of abstractions and high-level languages; as a result, people often have a weak understanding of how certain concepts work, such as pointers, if they do not understand how it is implemented in machine language (Nakano and Ito, 2008). Furthermore, the concept of the fetch-decode-execute cycle only helps to abstract the CPU further, boiling down the entire process into three words and failing to emphasise the complexity of each stage and the coordination required.
Through the creation of the CPU, a much richer understanding of how a computer system works as a unit was gained but most importantly it helped to showcase the intricacies of how a CPU performs its tasks, illustrating how an instruction set can be mapped onto an underlying architecture. The synergy between the instruction set and the silicon below it is often overlooked, but without it modern day computing would not be a reality.
6 Reflective Analysis
It is important to note that the project had deviated from the original proposal of attempting to make cycle-accurate versions of the MOS 6502 and the Manchester Baby – the change was a natural progression after having seen how quickly I had implemented a traffic light circuit based on a counter and decoder combination. Despite not being anywhere near the complexity of a CPU, it had showed me that the language was easy to work with and that I understood, to an extent, how circuits can be made.
Ultimately the project was a success – the processor is capable of computation as shown by the Fibonacci sequence, and the output has a meaningful use as it can be stored into VRAM to display on a monitor; unfortunately, the I/O is very rudimentary, and would have definitely benefited from some form of input – a keyboard at minimum – to enable more possibilities such as playing a game or navigating some menus. This additional feature would require a modification to the processor in order to implement an interrupt handler, alongside with a method to handle the input itself – such as memory mapping the keyboard or having some method of polling it.
The development side of the project provided me with invaluable knowledge of how to design and test circuits from scratch using HDLs, alongside with learning a vendor suite means that I am now aware of the process it takes to transfer a design from HDL onto physical silicon. Despite being locked into one vendor for the entirety of the project, this project has provided transferrable skills such as debugging, understanding appropriate pin assignments, and overall understanding what Verilog is capable of.
I think the success of the project can be partially attributed to the abstractions and ease of use that Verilog provides – the C-like syntax certainly helps in easing the learning curve (at least in my case) but there are things to get used to such as new ideas like as a sensitivity list or having to define the direction of a parameter (i.e. input or output) or understanding the difference between a blocking & non-blocking assignment, and having to get past the quirks of using “begin” and “end” instead of the regular curly brackets in every other C-like language.
Furthermore, debugging is a completely different experience when compared to regular software development; there is no concept of a breakpoint or being able to step through the code so you are forced to use simulation software to plot waveforms in order for you to analyse the behaviour and try to make some sense of this – it gets really difficult in a complex system as there are so many sub-modules and possibly 20 to 30+ different signals to keep track of.
Given another chance to do this project, there are a multitude of things I would change about this particular implementation.
The CPU architecture is incredibly simple – it lacks any form of the traditional busses you may see in a typical CPU that is out on the market right now, which makes connecting things like the ALU and registers together incredibly tedious – there are ~3 wires to connect so that it functions, but that is without having to rework the multiplexers and de-multiplexer at both ends of the ALU.
Furthermore, the CPU is not pipelined – every instruction has to finish before the next one is even fetched. This results in increased execution time as when one instruction was busy being executed, another could have been fetched and decoded. Obviously for a small scale project the execution time does not matter much as it will never be used in a time-sensitive situation, but pipelining is a key feature of modern day CPUs and it is important to understand how it works.
Additionally, the CPU lacks any form of floating-point operations, making floating-point math basically impossible – unless you attempted to use fixed-point math however it is not quite clear on how feasible it would be or how easy it would be to implement with the current instruction set of the architecture.
Although it would be a very advanced feature to implement, some form of branch prediction would be fascinating to see – unfortunately, there is not much information out about how a branch predictor is implemented so it is unclear how it would fit in with the project processor.
Unlike x86 with its MASM and NASM, the project CPU lacks any form of an assembler – the key component in translating assembly code into the machine-specific code which could eventually provide the foundations for a toolchain for higher, more abstracted languages to be implemented. Unfortunately, it was not in the scope of this project to make one as it would take too much time away from other studies, but also from the CPU itself. This does mean that any program written for the CPU has to be written in its machine code, which is both tedious and very error prone – for example, modern assemblers provide features such as labels which allow the programmer to denote a particular memory location with some form of symbol to which they can refer to later however, in the case for this CPU, there are no such features since you are working with machine code directly, so it is up to you to ensure that the correct memory locations are being referenced. Not only is writing the code tedious, but debugging is only possible with the use of software like ModelSim to plot the waveforms and then analysing them to see what is wrong.
I do not think that I would have learned as much about CPU design if I had copied an existing model – there are countless intricate details which need to be considered for all of the digital machinery to function in harmony.
The CPU is fully open-source and is available at https://github.com/krisjdev/tau-processor
Bibliography
Xilinx (n.d. (a)). “What is an FPGA?”. Available from https://www.xilinx.com/products/silicon-devices/fpga/what-is-an-fpga.html (accessed 9 November 2021).
Nakano, K. and Ito, Y. (2008). “Processor, Assembler, and Compiler Design Education using an FPGA”. Available from https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=4724385 (accessed 14 November 2021).
Tong, Jason G., Anderson, Ian D. L. and Khalid, Mohammed A. S. (2006). “Soft-core Processors for Embedded Systems”. Available from https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=4243676 (accessed 15 November 2021).
Lee, J. H., Lee, S. E., Yu, H. C., Suh, T. (2012). “Pipelined CPU Design With FPGA in Teaching Computer Architecture”. Available from https://ieeexplore.ieee.org/document/6093707 (accessed 18 February 2022).
Yıdız, A., Ugurdag, H. F., Aktemur, B., İskender, D., Gören, S. (2018). “CPU Design Simplified”. Available from https://ieeexplore.ieee.org/document/8566475 (accessed 18 February 2022).
Microsemi. (n.d.). “Soft CPUs”. Available from https://www.microsemi.com/product-directory/mi-v-ecosystem/5093-other-cpus (accessed 19 February 2022).
Fox, C. (n.d.). “Computer Architecture: from the stone age to the quantum age”. No Starch Press, San Francisco, in press.
Eljhani, M. M. and Kepuska, V. Z. (2021). “Reduced Instruction Set Computer Design on FPGA”. Available from https://ieeexplore.ieee.org/document/9464409 (accessed 19 February 2022).
Yhang, Y. and Bao, L. (2011). “The Design of an 8-bit CISC CPU Based on FPGA”. Available from https://ieeexplore.ieee.org/document/6040633 (accessed 20 February 2022).
Koopman, P. (1989). “What is a stack?”. Available from https://users.ece.cmu.edu/~koopman/stack_computers/sec1_2.html (accessed 19 February 2022).
Monk, S. (2017). “Programming FPGAs: Getting Started with Verilog”. New York: McGraw Hill.
TinyVGA. (2008). “VGA Signal 640 x 480 @ 60 Hz Industry standard timing”. Available from http://www.tinyvga.com/vga-timing/640x480@60Hz (accessed 15 May 2022).
PCMag. (n.d. (a)). “specialized processor”. Available from https://www.pcmag.com/encyclopedia/term/specialized-processor (accessed 2 May 2022).
ARM. (n.d. (a)). “Instruction Set Architecture (ISA)”. Available from https://www.arm.com/glossary/isa (accessed 3 May 2022).
Null, L. and Lobur, J. (2018). “Essentials of Computer Organization and Architecture”, Fifth Edition. Burlington: Jones & Bartlett Learning.
ARM. (2005). “ARM Architecture Reference Manual”. Available from https://documentation-service.arm.com/static/5f8dacc8f86e16515cdb865a (accessed 5 May 2022).
Intel. (2021). “Intel 64 and IA-32 Architectures Software Developer’s Manual – Combined Volumes: 1, 2A, 2B, 2C, 2D, 3A, 3B, 3C, 3D and 4”. Available from https://www.intel.com/content/www/us/en/developer/articles/technical/intel-sdm.html (accessed 14 April 2022).
MOS. (1976). “MCS6500 MICROCOMPUTER FAMILY PROGRAMMING MANUAL”. Available from http://archive.6502.org/books/mcs6500_family_programming_manual.pdf (accessed 20 May 2022).
Wilson, P. and Mantooth, H. A. (2013). “Model-Based Engineering for Complex Electronic Systems”. Oxford: Elsevier.
Eigenmann, R. and Lilja, D. (1998). “Von Neumann Computers”. Available from http://public.callutheran.edu/~reinhart/CSC521/Week3/VonNeumann.pdf (accessed 7 May 2022).
IBM. (2022). “Absolute addressing”. Available from https://www.ibm.com/docs/en/aix/7.2?topic=addressing-absolute (accessed 10 May 2022).
nandland. (n.d.). “What is a Block RAM (BRAM) in an FPGA? Tutorial for beginners”. Available from https://www.nandland.com/articles/block-ram-in-fpga.html (accessed 10 May 2022).
PCMag (n.d. (b)) “glue logic”. Available from https://www.pcmag.com/encyclopedia/term/glue-logic (accessed 10 May 2022).
Harrison, J. (n.d.) “Formal verification”. Available from https://www.cl.cam.ac.uk/~jrh13/papers/mark10.pdf (accessed 16 May 2022).
Chandra, P. and Weisstein, E. W. (2022). “Fibonacci Number”. Available from https://mathworld.wolfram.com/FibonacciNumber.html (accessed 17 May 2022).
IBM. (1995) “6 Measuring Performance”. Available from https://u.cs.biu.ac.il/~wisemay/co/co6.pdf (accessed 18 May 2022).
Appendix A
Presented below is the implemented instruction set of the processor. Some notes:
- For instructions where there is an immediate value, the opcode range indicates which register the CPU will target. For example,
mov a, imm8has an opcode of28h, andmov b, imm8will have an opcode of29h- this is repeated for all registers (8 total - A, B, C, D, E, F, G & H). - Some instructions combine the values from registers for their own purpose, this is presented with curly braces e.g.,
{E, F}indicates that the contents of the E and F registers are concatenated together i.e., ifE = 0xbeandF = 0xefthen{E, F} = 0xbeef. - There are four ALU flags - Zero (Z), Sign (S), Carry (C) and Overflow (O). They are referred to by their letter.
- On a failed conditional jump, the program counter will always be incremented by two.
| Opcode (Base 16) |
Mnemonic | Action | ALU Flags Affected |
|---|---|---|---|
| 00 | nop |
Nothing is executed for one machine cycle | None |
| 01 | hlt |
Stops execution completely - machine must be reset | None |
| 02 | load |
Indexes system memory at address {E, F} and stores the value in {G, H} |
None. |
| 03 | store |
Stores value of {G, H} in system memory at address {E, F} |
None |
| 04 | loadv |
Indexes video memory at address {E, F} and stores value in {G, H} |
None |
| 05 | storev |
Stores value of {G, H} in video memory at address {E, F} |
None |
| 06 | mov reg1, reg2 |
reg = reg2 |
None |
| 07 | cmp reg1, reg2 |
Compare if reg1 == reg2 by performing reg1 - reg2. Does not affect the registers |
Z, S, C, O |
| 08 | test reg1, reg2 |
Performs bitwise AND on reg1 and reg2 |
Z, S. C & O = 0 |
| 09 | shl reg1, reg2 |
reg1 = reg1 << reg2 |
Z, S, C |
| 0A | shr reg1, reg2 |
reg1 = reg1 >> reg2 |
Z, S, C |
| 0B | add reg1, reg2 |
reg1 = reg1 + reg2 |
Z, S, C, O |
| 0C | adc reg1, reg2 |
reg1 = reg1 + reg2 + C |
Z, S, C, O |
| 0D | sub reg1, reg2 |
reg1 = reg1 - reg2 |
Z, S, C, O |
| 0E | sbb reg1, reg2 |
reg1 = reg1 - (reg2 + C) |
Z, S, C, O |
| 0F | mul reg1, reg2 |
reg1 = reg1 * reg2 |
Z, S |
| 10 | and reg1, reg2 |
reg1 = reg1 & reg2 |
Z, S. C & O = 0 |
| 11 | or reg1, reg2 |
reg1 = reg1 | reg2 |
Z, S. C & O = 0 |
| 12 | xor reg1, reg2 |
reg1 = reg1 ^ reg2 |
Z, S. C & O = 0 |
| 13 | not reg1 |
reg1 = ~reg1 |
None |
| 14 | jmp [address] |
Unconditional jump - program counter = address |
None |
| 15 | je [address] |
program counter = address if Z = 1 |
None |
| 16 | jne [address] |
program counter = address if Z = 0 |
None |
| 17 | jc [address] |
program counter = address if C = 1 |
None |
| 18 | jnc [address] |
program counter = address if C = 0 |
None |
| 19 | js [address] |
program counter = address if S = 1 |
None |
| 1A | jns [address] |
program counter = address if S = 0 |
None |
| 1B | jo [address] |
program counter = address if O = 1 |
None |
| 1C | jno [address] |
program counter = address if O = 0 |
None |
| 1D | ja [address] |
program counter = address if C ^ Z = 0 |
None |
| 1E | jae [address] |
program counter = address if C = 0 |
None |
| 1F | jb [address] |
program counter = address if C = 1 |
None |
| 20 | jbe [address] |
program counter = address if C | Z = 1 |
None |
| 21 | jg [address] |
program counter = address if (S ^ O) | Z = 0 |
None |
| 22 | jge [address] |
program counter = address if S ^ O = 0 |
None |
| 23 | jl [address] |
program counter = address if S ^ O = 1 |
None |
| 24 | jle [address] |
program counter = address if (S ^ O) | Z = 1 |
None |
| 25, 26, 27 | undefined |
nop |
None |
| 28 to 2F | mov a-h, imm8 |
reg1 = imm8 |
None |
| 30 to 37 | cmp a-h, imm8 |
Compare if reg1 == imm8 by performing reg1 - imm8. Does not affect registers |
Z, S, C, O |
| 38 to 3F | test a-h, imm8 |
Performs bitwise AND on reg1 and imm8 |
Z, S. C & O = 0 |
| 40 to 47 | shl a-h, imm8 |
reg1 = reg1 << imm8 |
Z, S, C |
| 48 to 4F | shr a-h, imm8 |
reg1 = reg1 >> imm8 |
Z, S, C |
| 50 to 57 | add a-h, imm8 |
reg1 = reg1 + imm8 |
Z, S, C, O |
| 58 to 5F | adc a-h, imm8 |
reg1 = reg1 + imm8 + C |
Z, S, C, O |
| 60 to 67 | sub a-h, imm8 |
reg1 = reg1 - imm8 |
Z, S, C, O |
| 68 to 6F | sbb a-h, imm8 |
reg1 = reg1 - (imm8 + C) |
Z, S, C, O |
| 70 to 77 | mul a-h, imm8 |
reg1 = reg1 * imm8 |
Z, S |
| 78 to 7F | and a-h, imm8 |
reg1 = reg1 & imm8 |
Z, S. C & O = 0 |
| 80 to 87 | or a-h, imm8 |
reg1 = reg1 | imm8 |
Z, S. C & O = 0 |
| 88 to 8F | xor a-h, imm8 |
reg1 = reg1 ^ imm8 |
Z, S. C & O. |